RhoSimpleFoam
rhoSimpleFoam
rhoSimpleFoam is a steady-state solver for compressible, turbulent flow, using the SIMPLE (Semi-Implicit Method for Pressure Linked Equations) algorithm. In the newer releases it also includes an option to use the SIMPLEC (Semi-Implicit Method for Pressure Linked Equations Consistent) algorithm. It is a pressure based compressible solver. That means that a pressure equation is solved and the density is related to the pressure via an equation of state.
Contents
[hide]1 Solution Strategy
The solver follows a segregated solution strategy. This means that the equations for each variable characterizing the system (the velocity 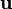 , the pressure
, the pressure 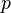 , the energy (either internal energy or enthalpy depending on the choice of the user) and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
, the energy (either internal energy or enthalpy depending on the choice of the user) and the variables characterizing turbulence) is solved sequentially
and the solution of the preceding equations is inserted in the subsequent equation. The non-linearity appearing in the momentum equation (the face flux
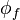 which is a function of the velocity and density
which is a function of the velocity and density 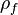 ) is resolved by computing it from the velocity and pressure values of the preceding iteration. Note that the density is related to the pressure via an equation of state which can be selected by the user. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field
) is resolved by computing it from the velocity and pressure values of the preceding iteration. Note that the density is related to the pressure via an equation of state which can be selected by the user. The dependence from
the pressure is introduced to avoid a decoupling between the momentum and pressure equations and hence the appearance of high frequency oscillation in the solution (check board effect).
The first equation to be solve is the momentum equation. It delivers a velocity field 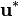 which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the energy equation is solved. Then that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field
which is in general not divergence free, i.e.
it does not satisfy the continuity equation. After that the energy equation is solved. Then that the momentum and the continuity equations are used to construct an equation for the pressure. The
aim is to obtain a pressure field 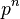 , which, if inserted in the momentum equation, delivers a divergence free velocity field
, which, if inserted in the momentum equation, delivers a divergence free velocity field 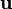 .
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
.
After correcting the velocity field, the equations for turbulence are solved.
The above iterative solution procedure is repeated until convergence.
A good book which describes the derivation of the pressure equation for compressible cases is the one of [1].
To summarize the solution algorithm is as follows
- Compute an intermediate velocity
 by means of the momentum equation. This velocity (together with the density
by means of the momentum equation. This velocity (together with the density 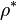 does not satisfy the continuity equation
does not satisfy the continuity equation
- Compute energy equation. The compressibilty
 is updated too by the thermodynamic packaged (of course also the temperature the viscosity).
is updated too by the thermodynamic packaged (of course also the temperature the viscosity).
- Compute the pressure
 which satisfies the momentum and also the continuity equation.
which satisfies the momentum and also the continuity equation.
- Correct the velocity and face flux which satisfy the continuity equation
- Update the density

- Update the turbulence quantities
- If not converged go to the beginning of the iteration
The source code can be found in rhoSimpleFoam.C
int main(int argc, char *argv[]) { argList::addNote ( "Steady-state solver for compressible turbulent flow." ); #include "postProcess.H" #include "addCheckCaseOptions.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMesh.H" #include "createControl.H" #include "createFields.H" #include "createFieldRefs.H" #include "initContinuityErrs.H" turbulence->validate(); // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // Info<< "\nStarting time loop\n" << endl; while (simple.loop()) { Info<< "Time = " << runTime.timeName() << nl << endl; // Pressure-velocity SIMPLE corrector #include "UEqn.H" #include "EEqn.H" if (simple.consistent()) { #include "pcEqn.H" } else { #include "pEqn.H" } turbulence->correct(); runTime.write(); runTime.printExecutionTime(Info); } Info<< "End\n" << endl; return 0; }
2 Equations
In the next section the equation to be solved are described. In contrast to incompressible fluids, where the density is constant, in compressible flows the density varies in space and time, i.e., it the density became a thermodynamic property. For a pure mixture the thermodynamic state is fully described by to variables, i.e.,  the density is a function of the pressure and the temperature. For this reason in compressible flows we need to solve besides the equations for the momentum and the pressure (which is derived from the continuity equations) also an equation which gives us the evolution of the temperature. We will see later that the temperature is obtained via a thermodynamic relation after we solved the energy equation. After that, the density
the density is a function of the pressure and the temperature. For this reason in compressible flows we need to solve besides the equations for the momentum and the pressure (which is derived from the continuity equations) also an equation which gives us the evolution of the temperature. We will see later that the temperature is obtained via a thermodynamic relation after we solved the energy equation. After that, the density 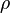 can be obtained from the other two variables via an equation of state.
can be obtained from the other two variables via an equation of state.
2.1 Momentum Equation
The equation of motion in rhosimpleFoam are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
-
 | (1) |
 represents the velocity in the relative reference frame,
represents the velocity in the relative reference frame,  is the velocity described in the inertial reference frame,
is the velocity described in the inertial reference frame,  is the angular velocity of the moving reference frame,
is the angular velocity of the moving reference frame,  is the sum of the viscous and turbulent stress tensor. It is evident that the above equation can be interpreted as the Favre averaged Navier Stokes equation rather than the Reynolds averaged Navier stokes equation. Favre averaging is a transformation which avoids the appearance of correlation involving the density fluctuations in the continuity and momentum equation. For a more detailed discussion see the thread https://www.cfd-online.com/Forums/openfoam-solving/193246-favre-reynolds-average-openfoam.html or the book of [2].
is the sum of the viscous and turbulent stress tensor. It is evident that the above equation can be interpreted as the Favre averaged Navier Stokes equation rather than the Reynolds averaged Navier stokes equation. Favre averaging is a transformation which avoids the appearance of correlation involving the density fluctuations in the continuity and momentum equation. For a more detailed discussion see the thread https://www.cfd-online.com/Forums/openfoam-solving/193246-favre-reynolds-average-openfoam.html or the book of [2].
The source code can be found in the file UEqn.H:
// Solve the Momentum equation
MRF.correctBoundaryVelocity(U);
tmp<fvVectorMatrix> tUEqn
(
fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence->divDevRhoReff(U)
==
fvOptions(rho, U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
UEqn.relax();
fvOptions.constrain(UEqn);
solve(UEqn == -fvc::grad(p));
fvOptions.correct(U);Note that the above equation differs from the equations without considering a moving frame of reference in two terms:  which if interpolated on the face of the control volume gives the relative face flux and the term
which if interpolated on the face of the control volume gives the relative face flux and the term  which is simply a explicit source term in the momentum equation. We will see later in the pressure equation how the relative face flux is calculated.
which is simply a explicit source term in the momentum equation. We will see later in the pressure equation how the relative face flux is calculated.
The source code of the acceleration resulting from the description in a moving frame of reference can be found in the following src/finiteVolume/cfdTools/general/MRF/MRFZoneList.C
Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt ( const volVectorField& U ) const { tmp<volVectorField> tacceleration ( new volVectorField ( IOobject ( "MRFZoneList:acceleration", U.mesh().time().timeName(), U.mesh() ), U.mesh(), dimensionedVector(U.dimensions()/dimTime, Zero) ) ); volVectorField& acceleration = tacceleration.ref(); forAll(*this, i) { operator[](i).addCoriolis(U, acceleration); } return tacceleration; } Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt ( const volScalarField& rho, const volVectorField& U ) const { return rho*DDt(U); }
The calculation of the Coriolis force is done in the file src/finiteVolume/cfdTools/general/MRF/MRFZone.C
void Foam::MRFZone::addCoriolis ( const volVectorField& U, volVectorField& ddtU ) const { if (cellZoneID_ == -1) { return; } const labelList& cells = mesh_.cellZones()[cellZoneID_]; vectorField& ddtUc = ddtU.primitiveFieldRef(); const vectorField& Uc = U; const vector Omega = this->Omega(); forAll(cells, i) { label celli = cells[i]; ddtUc[celli] += (Omega ^ Uc[celli]); } }
The way the turbulent stresses enter into the momentum equation is well described here: https://www.openfoam.com/documentation/guides/latest/doc/guide-turbulence-ras.html.
2.2 Energy Equation
The derivation of the Favre agraged energy equation for compressible flows can be found in the book of [3]. A description of the terms resulting in the energy equation from the favre averaging can also be found in https://www.cfd-online.com/Wiki/Favre_averaged_Navier-Stokes_equations. The following equation are taken from [4].

The total energy  is defined as follows:
is defined as follows:
 . The overline
. The overline  denotes the Reynolds averaging, the tilde the Favre averaging, k the turbulent kinetic energy and the two
denotes the Reynolds averaging, the tilde the Favre averaging, k the turbulent kinetic energy and the two  denote the fluctuation due to the Favre averaging:
denote the fluctuation due to the Favre averaging:
 .
.
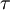 is the viscous stress tensor.
is the viscous stress tensor.
If we neglect the turbulent kinetic energy in the total energy and the last three terms of the above equation (together with the time derivative since rhoSimpleFoam is a steady solver) we get:

If we insert the definition of the enthalpy h:

in the above equation we get the following equation:

The total heat flux  is the sum of viscous and turbulent heat flux
is the sum of viscous and turbulent heat flux  .
It is calculated as follows in case the sensible enthalpy is chosen as quantity solved for:
.
It is calculated as follows in case the sensible enthalpy is chosen as quantity solved for:

and as follows if the sensible internal energy is chosen as quantity solved for:

The reason is to have the same equation whether one solves for e or h. The way this is achieved can be found in the following discussion: https://www.cfd-online.com/Forums/openfoam/232183-question-about-fvm-laplacian-turbulence-alphaeff-he-rhosimplefoam.html.
Differences between the two equation arise in the numerical stability. Since for the two equation two different explicit source terms appear, one equation may be more stable compared to the other depending on the magnitude and sign of the explicit source term. Also here a discussion can be found here: https://www.cfd-online.com/Forums/openfoam-solving/228152-when-choose-sensibleinternalenergy-sensibleenthalpy-thermophysicalproperties.html.
The equation solved can be found in the file EEqn.H
{ volScalarField& he = thermo.he(); fvScalarMatrix EEqn ( fvm::div(phi, he) + ( he.name() == "e" ? fvc::div(phi, volScalarField("Ekp", 0.5*magSqr(U) + p/rho)) : fvc::div(phi, volScalarField("K", 0.5*magSqr(U))) ) - fvm::laplacian(turbulence->alphaEff(), he) == fvOptions(rho, he) ); EEqn.relax(); fvOptions.constrain(EEqn); EEqn.solve(); fvOptions.correct(he); thermo.correct(); }
2.2.1 Correction of the thermodynamic properties
After that the energy equation is solved, the thermodynamic properties of the fluid are updated. This is done by the following code line:
thermo.correct();To elucidate what is done exactly we'll take the hePsiThermo package as example. In this package the density is related to the pressure via the compressibilty  .
.
The function correct looks like this (see the file $FOAM_SCR/thermophysicalModels/basic/psiThermo/hePsiThermo.C):
template<class BasicPsiThermo, class MixtureType> void Foam::hePsiThermo<BasicPsiThermo, MixtureType>::correct() { DebugInFunction << endl; calculate ( this->p_, this->T_, this->he_, this->psi_, this->mu_, this->alpha_, false // No need to update old times ); DebugInFunction << "Finished" << endl; } template<class BasicPsiThermo, class MixtureType> void Foam::hePsiThermo<BasicPsiThermo, MixtureType>::calculate ( const volScalarField& p, volScalarField& T, volScalarField& he, volScalarField& psi, volScalarField& mu, volScalarField& alpha, const bool doOldTimes ) { // Note: update oldTimes before current time so that if T.oldTime() is // created from T, it starts from the unconverted T if (doOldTimes && (p.nOldTimes() || T.nOldTimes())) { calculate ( p.oldTime(), T.oldTime(), he.oldTime(), psi.oldTime(), mu.oldTime(), alpha.oldTime(), true ); } const scalarField& hCells = he.primitiveField(); const scalarField& pCells = p.primitiveField(); scalarField& TCells = T.primitiveFieldRef(); scalarField& psiCells = psi.primitiveFieldRef(); scalarField& muCells = mu.primitiveFieldRef(); scalarField& alphaCells = alpha.primitiveFieldRef(); forAll(TCells, celli) { const typename MixtureType::thermoType& mixture_ = this->cellMixture(celli); if (this->updateT()) { TCells[celli] = mixture_.THE ( hCells[celli], pCells[celli], TCells[celli] ); } psiCells[celli] = mixture_.psi(pCells[celli], TCells[celli]); muCells[celli] = mixture_.mu(pCells[celli], TCells[celli]); alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]); } const volScalarField::Boundary& pBf = p.boundaryField(); volScalarField::Boundary& TBf = T.boundaryFieldRef(); volScalarField::Boundary& psiBf = psi.boundaryFieldRef(); volScalarField::Boundary& heBf = he.boundaryFieldRef(); volScalarField::Boundary& muBf = mu.boundaryFieldRef(); volScalarField::Boundary& alphaBf = alpha.boundaryFieldRef(); forAll(pBf, patchi) { const fvPatchScalarField& pp = pBf[patchi]; fvPatchScalarField& pT = TBf[patchi]; fvPatchScalarField& ppsi = psiBf[patchi]; fvPatchScalarField& phe = heBf[patchi]; fvPatchScalarField& pmu = muBf[patchi]; fvPatchScalarField& palpha = alphaBf[patchi]; if (pT.fixesValue()) { forAll(pT, facei) { const typename MixtureType::thermoType& mixture_ = this->patchFaceMixture(patchi, facei); phe[facei] = mixture_.HE(pp[facei], pT[facei]); ppsi[facei] = mixture_.psi(pp[facei], pT[facei]); pmu[facei] = mixture_.mu(pp[facei], pT[facei]); palpha[facei] = mixture_.alphah(pp[facei], pT[facei]); } } else { forAll(pT, facei) { const typename MixtureType::thermoType& mixture_ = this->patchFaceMixture(patchi, facei); if (this->updateT()) { pT[facei] = mixture_.THE(phe[facei], pp[facei], pT[facei]); } ppsi[facei] = mixture_.psi(pp[facei], pT[facei]); pmu[facei] = mixture_.mu(pp[facei], pT[facei]); palpha[facei] = mixture_.alphah(pp[facei], pT[facei]); } } } }
We see from the above code that first the temperature is retrieved from the enthalpy or internal energy. For a good explanation how it's done exactly see https://caefn.com/openfoam/temperature-calculation. After that the temperature dependent variables like the dynamic viscosity 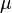 , the compresibility
, the compresibility  and the thermal diffusivity
and the thermal diffusivity 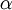 are calculated.
are calculated.
2.3 Pressure Equation
Note that a easy to understand derivation of the pressure or pressure correction equations for compressible flows can be found in [5].
The derivation of the pressure pressure equation is very similar to the one used for the incompressbile case (see e.g. https://openfoamwiki.net/index.php/SimpleFoam).
Also here after the solution of the momentum equation we get a velocity  and a density
and a density  (that's the main difference to the incompressible case) at the point P which together do not satisfy the continuity equation. In semi discrete form the mass flux at the point P
(that's the main difference to the incompressible case) at the point P which together do not satisfy the continuity equation. In semi discrete form the mass flux at the point P  can be written as:
can be written as:
![m_P^* = \rho_P^*\bold{u_P^*} = \rho_P^* \frac{\bold {H[u^*] }}{a_P^* } - \rho_P^*\frac{\nabla p_P^{n-1}}{a_P^* }](/images/math/c/4/4/c449c78a34bdc41c0cff68311bc10223.png) |
Now we want to add a velocity correction  , a density correction
, a density correction  and a pressure correction
and a pressure correction  in order that the continuity equation is satisfied:
in order that the continuity equation is satisfied:
![m_P = (\rho_P^* + \rho_P^')(\bold{u_P^*} + \mathbf{u_p^'}) = (\rho_P^* + \rho_P^')(\frac{\bold {H[u^*] }}{a_P^* } + \frac{\bold {H[u^'] }}{a_P^* } )- (\rho_P^* + \rho_P^') (\frac{\nabla p_P^{n-1}}{a_P^* } - \frac{\nabla p_P^'}{a_P^* })](/images/math/6/7/7/677da0a9df5d78ae0ce4deb1f8da507a.png) |
After applying the following definition to the above equation  ,
,  :
:
![m_P = (\rho_P^* + \underbrace{\Psi p_P - \Psi p_P^{n-1}}_{\rho_P^'} )(\frac{\bold {H[u^*] }}{a_P^* } + \frac{\bold {H[u^'] }}{a_P^* } ) - (\rho_P^* + \rho_P^') \frac{\nabla p_P}{a_P^* }](/images/math/e/b/9/eb9c6ec2eb6263cb3fd2d9e020e2c0e5.png) |
If we interpolate the above relation to the cell faces, sum the above equation over all faces of the control volume and neglect the density correction in front of the pressure term we get a equation for the pressure:
![\sum_f m_P|_f = 0 = \sum_f (\rho_P^* + \underbrace{\Psi p_P - \Psi p_P^{n-1}}_{\rho_P^'} )(\frac{\bold {H[u^*] }}{a_P^* } + \rho_P^*\frac{\bold {H[u^'] }}{a_P^* } ) |_f - \sum_f\rho_P^*\frac{\nabla p_P}{a_P^* } |_f](/images/math/f/5/5/f554aebb2de01617cd08e75224264c3b.png) |
Note that the contribution of the neighboring cells to the velocity correction ![\bold {H[u'] }](/images/math/5/5/0/550565cfeb9ce06507409f03af2bacb5.png) is still unknown and has to be approximated. Different approximation are used in the simple algorithm family. In the following the two available in rhoSimpleFoam are described.
is still unknown and has to be approximated. Different approximation are used in the simple algorithm family. In the following the two available in rhoSimpleFoam are described.
2.3.1 Simple
If we neglect the contribution of the neighbours of the velocity correction (i.e. we set ![\bold {H[u'] } = 0](/images/math/4/8/c/48c782a087e13ca25277df5340ac0323.png) ) we get the pressure equation solved in the simple
algorithm.
) we get the pressure equation solved in the simple
algorithm.
In this way we get following equation:
![\sum_f (\rho_P^* + \underbrace{\Psi p_P - \Psi p_P^{n-1}}_{\rho_P^'} )(\frac{\bold {H[u^*] }}{a_P^* } ) |_f - \sum_f\rho_P^*\frac{\nabla p_P}{a_P^* } |_f = 0](/images/math/c/7/0/c707e545fdd852158d134d1c578c116f.png) |
From the above equation we notice that the pressure equation has also a convective term (the finite volume discretisation of the divergence is a sum over the cell volumes). For high Mach number flows this convective term transforms the equation for the pressure from a elliptical equation in a hyperbolic equation [6].
In case the transonic switch in the fvSolution dictionary is set to false, the contribution of the density correction 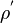 is neglected. For this reason the transonic switch has to be set to false only for low Mach number flow where density fluctuations are small.
is neglected. For this reason the transonic switch has to be set to false only for low Mach number flow where density fluctuations are small.
The source code can be found in the file pEqn.H:
volScalarField rAU(1.0/UEqn.A()); surfaceScalarField rhorAUf("rhorAUf", fvc::interpolate(rho*rAU)); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); tUEqn.clear(); bool closedVolume = false; surfaceScalarField phiHbyA("phiHbyA", fvc::interpolate(rho)*fvc::flux(HbyA)); MRF.makeRelative(fvc::interpolate(rho), phiHbyA); // Update the pressure BCs to ensure flux consistency constrainPressure(p, rho, U, phiHbyA, rhorAUf, MRF); if (simple.transonic()) { surfaceScalarField phid ( "phid", (fvc::interpolate(psi)/fvc::interpolate(rho))*phiHbyA ); phiHbyA -= fvc::interpolate(psi*p)*phiHbyA/fvc::interpolate(rho); while (simple.correctNonOrthogonal()) { fvScalarMatrix pEqn ( fvc::div(phiHbyA) + fvm::div(phid, p) - fvm::laplacian(rhorAUf, p) == fvOptions(psi, p, rho.name()) ); // Relax the pressure equation to ensure diagonal-dominance pEqn.relax(); pEqn.setReference ( pressureControl.refCell(), pressureControl.refValue() ); pEqn.solve(); if (simple.finalNonOrthogonalIter()) { phi = phiHbyA + pEqn.flux(); } } } else { closedVolume = adjustPhi(phiHbyA, U, p); while (simple.correctNonOrthogonal()) { fvScalarMatrix pEqn ( fvc::div(phiHbyA) - fvm::laplacian(rhorAUf, p) == fvOptions(psi, p, rho.name()) ); pEqn.setReference ( pressureControl.refCell(), pressureControl.refValue() ); pEqn.solve(); if (simple.finalNonOrthogonalIter()) { phi = phiHbyA + pEqn.flux(); } } } #include "incompressible/continuityErrs.H" // Explicitly relax pressure for momentum corrector p.relax(); U = HbyA - rAU*fvc::grad(p); U.correctBoundaryConditions(); fvOptions.correct(U); bool pLimited = pressureControl.limit(p); // For closed-volume cases adjust the pressure and density levels // to obey overall mass continuity if (closedVolume) { p += (initialMass - fvc::domainIntegrate(psi*p)) /fvc::domainIntegrate(psi); } if (pLimited || closedVolume) { p.correctBoundaryConditions(); } rho = thermo.rho(); if (!simple.transonic()) { rho.relax(); }
2.3.2 Simplec
The starting point for the derivation of the simplec algorithm are the following two equations for the uncorrected velocity  and for the velocity correction
and for the velocity correction  :
:
![\bold{u_P^*} = \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* }](/images/math/2/2/2/2223c388faf5c26d534ecdf3784b4fcd.png) |
![\bold{u_P^'} = \frac{\bold {H[u^'] }}{a_P^* } - \frac{\nabla p_P^{'}}{a_P^* } = \frac{\sum_N \mathbf{a_N u_N^'}}{a_P^* } - \frac{\nabla p_P^{'}}{a_P^* }](/images/math/1/f/c/1fc27fdfa00cf71fbacebbb34e100aac.png) |
The scope is to add both equation and multiply them by  to get the corrected mass flux
to get the corrected mass flux  as function of the pressure (ore pressure correction) solely in order to obtain a solvable equation. The problem is that the second of the above equations involves also the neighboring contribution to the velocity at the point P. What we want is a explicit relation between
as function of the pressure (ore pressure correction) solely in order to obtain a solvable equation. The problem is that the second of the above equations involves also the neighboring contribution to the velocity at the point P. What we want is a explicit relation between  and
and  . To obtain such a relation we can approximate the velocity correction at the neighboring cells
. To obtain such a relation we can approximate the velocity correction at the neighboring cells  by the velocity at the cell center P
by the velocity at the cell center P  . For small cell sizes the two velocity should not differ too much and it is a good approximation. In this way we get:
. For small cell sizes the two velocity should not differ too much and it is a good approximation. In this way we get:
 |
 |
By doing so we get an explicit relation between the velocity correction  and the pressure correction
and the pressure correction  :
:
 |
Now we can use the above relation, sum it to the equation for the uncorrected velocity  and multiply it by the corrected density
and multiply it by the corrected density  :
:
![m_P = (\rho^* + \rho^') ( \mathbf{u_P^*} + \bold{u_P^'}) = (\rho^* + \rho^') ( \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{\nabla p_P^{'}}{a_P^* - \bold{H_1}} )](/images/math/5/3/5/53526ab5a34ce57652758f8b49393738.png) |
If we want to have a relation for the pressure  instead of the pressure correction
instead of the pressure correction  we can use following definition:
we can use following definition:
 |
Rearranged for  and inserted above we obtain:
and inserted above we obtain:
![m_P = (\rho^* + \underbrace{\rho^'}_{\Psi p_P - \Psi p_P^{n-1}}) ( \mathbf{u_P^*} + \bold{u_P^'}) = (\rho^* + \underbrace{\rho^'}_{\Psi p_P - \Psi p_P^{n-1}}) ( \frac{\bold {H[u^*] }}{a_P^* } - \frac{\nabla p_P^{n-1}}{a_P^* } - \frac{1 }{a_P^* - \bold{H_1}} (\nabla p_P- \nabla p_P^{n-1} ) )](/images/math/1/8/6/1866500b306208eb1f54649785c28272.png) |
If we neglect the contribution of the terms which involve the product of the density correction times the pressure terms we obtain:
![m_P = (\rho^* + \Psi p_P - \Psi p_P^{n-1}) ( \frac{\bold {H[u^*] }}{a_P^* }) - (\frac{\rho_P^*}{a_P^* } - \frac{\rho_P^*}{a_P^* - \bold{H_1}} ) \nabla p_P^{n-1} - \frac{\rho_P^*}{a_P^* - \bold{H_1}} \nabla p_P](/images/math/7/2/8/7281c6949401164d1910d10fbe578510.png) |
The final equation is obtained by summing over the faces of the control volume and setting it to zero:
![0 = \sum_f (\rho^* - \Psi p_P^{n-1}) ( \frac{\bold {H[u^*] }}{a_P^* })|_f + \sum_f ( \Psi p_P ) ( \frac{\bold {H[u^*] }}{a_P^* })|_f - \sum_f (\frac{\rho_P^*}{a_P^* } - \frac{\rho_P^*}{a_P^* - \bold{H_1}} ) \nabla p_P^{n-1}|_f - \sum_f\frac{\rho_P^*}{a_P^* - \bold{H_1}} \nabla p_P|_f](/images/math/3/7/b/37ba14718ce209c3d0319fb78a697292.png) |
The source code can be found in the file pcEqn.H:
rho = thermo.rho(); volScalarField rAU(1.0/UEqn.A()); volScalarField rAtU(1.0/(1.0/rAU - UEqn.H1())); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p)); tUEqn.clear(); bool closedVolume = false; surfaceScalarField phiHbyA("phiHbyA", fvc::interpolate(rho)*fvc::flux(HbyA)); MRF.makeRelative(fvc::interpolate(rho), phiHbyA); volScalarField rhorAtU("rhorAtU", rho*rAtU); // Update the pressure BCs to ensure flux consistency constrainPressure(p, rho, U, phiHbyA, rhorAtU, MRF); if (simple.transonic()) { surfaceScalarField phid ( "phid", (fvc::interpolate(psi)/fvc::interpolate(rho))*phiHbyA ); phiHbyA += fvc::interpolate(rho*(rAtU - rAU))*fvc::snGrad(p)*mesh.magSf() - fvc::interpolate(psi*p)*phiHbyA/fvc::interpolate(rho); HbyA -= (rAU - rAtU)*fvc::grad(p); while (simple.correctNonOrthogonal()) { fvScalarMatrix pEqn ( fvc::div(phiHbyA) + fvm::div(phid, p) - fvm::laplacian(rhorAtU, p) == fvOptions(psi, p, rho.name()) ); // Relax the pressure equation to maintain diagonal dominance pEqn.relax(); pEqn.setReference ( pressureControl.refCell(), pressureControl.refValue() ); pEqn.solve(); if (simple.finalNonOrthogonalIter()) { phi = phiHbyA + pEqn.flux(); } } } else { closedVolume = adjustPhi(phiHbyA, U, p); phiHbyA += fvc::interpolate(rho*(rAtU - rAU))*fvc::snGrad(p)*mesh.magSf(); HbyA -= (rAU - rAtU)*fvc::grad(p); while (simple.correctNonOrthogonal()) { fvScalarMatrix pEqn ( fvc::div(phiHbyA) - fvm::laplacian(rhorAtU, p) == fvOptions(psi, p, rho.name()) ); pEqn.setReference ( pressureControl.refCell(), pressureControl.refValue() ); pEqn.solve(); if (simple.finalNonOrthogonalIter()) { phi = phiHbyA + pEqn.flux(); } } } // The incompressible form of the continuity error check is appropriate for // steady-state compressible also. #include "incompressible/continuityErrs.H" // Explicitly relax pressure for momentum corrector p.relax(); U = HbyA - rAtU*fvc::grad(p); U.correctBoundaryConditions(); fvOptions.correct(U); bool pLimited = pressureControl.limit(p); // For closed-volume cases adjust the pressure and density levels // to obey overall mass continuity if (closedVolume) { p += (initialMass - fvc::domainIntegrate(psi*p)) /fvc::domainIntegrate(psi); } if (pLimited || closedVolume) { p.correctBoundaryConditions(); } rho = thermo.rho(); if (!simple.transonic()) { rho.relax(); }
3 References
- Jump up ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- Jump up ↑ Wilcox, David C. Turbulence modeling for CFD. Vol. 3. La Canada, CA: DCW industries, 2006.
- Jump up ↑ Wilcox, David C. Turbulence modeling for CFD. Vol. 3. La Canada, CA: DCW industries, 2006.
- Jump up ↑ Wilcox, David C. Turbulence modeling for CFD. Vol. 3. La Canada, CA: DCW industries, 2006.
- Jump up ↑ Moukalled, F., and M. Darwish. "A unified formulation of the segregated class of algorithms for fluid flow at all speeds." NUMERICAL HEAT TRANSFER PART B FUNDAMENTALS 37.1 (2000): 103-139.
- Jump up ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):


