ChtMultiRegionFoam
ChtMultiRegionFoam
Solver for steady or transient fluid flow and solid heat conduction, with conjugate heat transfer between regions, buoyancy effects, turbulence, reactions and radiation modelling.
Contents
[hide]1 Solution Strategy
The solver follows a segregated solution strategy. This means that the equations for each variable characterizing the system is solved sequentially and the solution of the preceding equations is inserted in the subsequent equation. The coupling between fluid and solid follows also the same strategy: First the equations for the fluid are solved using the temperature of the solid of the preceding iteration to define the boundary conditions for the temperature in the fluid. After that, the equation for the solid is solved using the temperature of the fluid of the preceding iteration to define the boundary condition for the solid temperature. This iteration procedure is executed until convergence.
The source code can be found in chtMultiRegionFoam.C
/*---------------------------------------------------------------------------*\ ========= | \\ / F ield | OpenFOAM: The Open Source CFD Toolbox \\ / O peration | Website: https://openfoam.org \\ / A nd | Copyright (C) 2011-2018 OpenFOAM Foundation \\/ M anipulation | ------------------------------------------------------------------------------- License This file is part of OpenFOAM. OpenFOAM is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. OpenFOAM is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with OpenFOAM. If not, see <http://www.gnu.org/licenses/>. Application chtMultiRegionFoam Description Solver for steady or transient fluid flow and solid heat conduction, with conjugate heat transfer between regions, buoyancy effects, turbulence, reactions and radiation modelling. \*---------------------------------------------------------------------------*/ #include "fvCFD.H" #include "turbulentFluidThermoModel.H" #include "rhoReactionThermo.H" #include "CombustionModel.H" #include "fixedGradientFvPatchFields.H" #include "regionProperties.H" #include "compressibleCourantNo.H" #include "solidRegionDiffNo.H" #include "solidThermo.H" #include "radiationModel.H" #include "fvOptions.H" #include "coordinateSystem.H" #include "pimpleMultiRegionControl.H" #include "pressureControl.H" // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // int main(int argc, char *argv[]) { #define NO_CONTROL #define CREATE_MESH createMeshesPostProcess.H #include "postProcess.H" #include "setRootCaseLists.H" #include "createTime.H" #include "createMeshes.H" #include "createFields.H" #include "initContinuityErrs.H" pimpleMultiRegionControl pimples(fluidRegions, solidRegions); #include "createFluidPressureControls.H" #include "createTimeControls.H" #include "readSolidTimeControls.H" #include "compressibleMultiRegionCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setInitialMultiRegionDeltaT.H" while (pimples.run(runTime)) { #include "readTimeControls.H" #include "readSolidTimeControls.H" #include "compressibleMultiRegionCourantNo.H" #include "solidRegionDiffusionNo.H" #include "setMultiRegionDeltaT.H" runTime++; Info<< "Time = " << runTime.timeName() << nl << endl; // --- PIMPLE loop while (pimples.loop()) { forAll(fluidRegions, i) { Info<< "\nSolving for fluid region " << fluidRegions[i].name() << endl; #include "setRegionFluidFields.H" #include "solveFluid.H" } forAll(solidRegions, i) { Info<< "\nSolving for solid region " << solidRegions[i].name() << endl; #include "setRegionSolidFields.H" #include "solveSolid.H" } } runTime.write(); Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << " s" << " ClockTime = " << runTime.elapsedClockTime() << " s" << nl << endl; } Info<< "End\n" << endl; return 0; } // ************************************************************************* //
2 Equations
For each region defined as fluid, the according equation for the fluid is solved and the same is done for each solid region. The regions are coupled by a thermal boundary condition. A short description of the solver can be found also in [1]
2.1 Equations Fluid
For each fluid region the compressible Navier Stokes equation are solved. The solver used to solve the fluid equations is a pressure bases solver. That means that a pressure equation (similar to the pressure equation used in an incompressible solver) is used to establish the connection between the momentum and the continuity equation. The algorithm to advance the solution in time is the following:
1. Update the density with the help of the continuity equation
2. Solve the momentum equation -> Here a velocity field 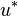 is computed which in general does not satisfy the continuity equation.
is computed which in general does not satisfy the continuity equation.
3. Solve the spices transport equation -> Here besides of the concentrations of the spices at the current time step the heat source due to chemical reaction 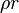 is
computed. The heat source therm is required in the energy equation.
is
computed. The heat source therm is required in the energy equation.
4. Solve the energy equation -> Here the temperature at the new time step is computed. The single regions in the domain are coupled via the temperature. Besides this, the temperature is required by the equation of state to compute the density 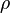 .
.
5. Solve the pressure equation to ensure mass conservation -> By means of the continuity and the momentum equation an equation for the pressure is constructed to generate a pressure field (and with the equation of state also a density field) which satisfies the continuity equation. Also a correction for the velocity is computed here which better satisfy the mass conservation.
6. Correct the density by means of the new pressure field and the equation of state
The source code can be found in solveFluid.H
if (pimple.frozenFlow()) { #include "EEqn.H" } else { if (!mesh.steady() && pimples.nCorrPimple() <= 1) { #include "rhoEqn.H" } #include "UEqn.H" #include "YEqn.H" #include "EEqn.H" // --- PISO loop while (pimple.correct()) { #include "pEqn.H" } if (pimples.pimpleTurbCorr(i)) { turbulence.correct(); } if (!mesh.steady() && pimples.finalIter()) { rho = thermo.rho(); } }
2.1.1 Mass conservation
The variable-density continuity equation is
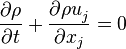 | (1) |
The source code can be found in src/finiteVolume/cfdTools/compressible/rhoEqn.H:
{ fvScalarMatrix rhoEqn ( fvm::ddt(rho) + fvc::div(phi) == fvOptions(rho) ); fvOptions.constrain(rhoEqn); rhoEqn.solve(); fvOptions.correct(rho); }
2.1.2 Momentum conservation
The equation of motion are written for a moving frame of reference. They are however formulated for the absolute velocity (the derivation of the equations of motion can be found in https://openfoamwiki.net/index.php/See_the_MRF_development and also in https://diglib.tugraz.at/download.php?id=581303c7c91f9&location=browse. Some additional information can be found in https://pingpong.chalmers.se/public/pp/public_courses/course07056/published/1497955220499/resourceId/3711490/content/UploadedResources/HakanNilssonRotatingMachineryTrainingOFW11-1.pdf):
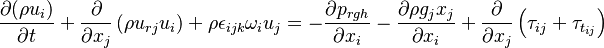 | (2) |
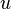 represent the velocity,
represent the velocity, 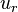 the relative veloicty,
the relative veloicty, 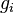 the gravitational acceleration,
the gravitational acceleration, 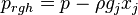 the pressure minus the hydrostatic pressure and
the pressure minus the hydrostatic pressure and
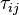 and
and 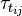 are the viscose and turbulent stresses. Note that since the relative velocity
are the viscose and turbulent stresses. Note that since the relative velocity 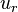 appears in the divergence term, the
face flux
appears in the divergence term, the
face flux 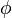 appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
appearing in the finite volume discretization of the momentum equation should be calculated with the relative velocity.
The source code can be found in Ueqn.H:
// Solve the Momentum equation
MRF.correctBoundaryVelocity(U);
tmp<fvVectorMatrix> tUEqn
(
fvm::ddt(rho, U) + fvm::div(phi, U)
+ MRF.DDt(rho, U)
+ turbulence.divDevRhoReff(U)
==
fvOptions(rho, U)
);
fvVectorMatrix& UEqn = tUEqn.ref();
UEqn.relax();
fvOptions.constrain(UEqn);
if (pimple.momentumPredictor())
{
solve
(
UEqn
==
fvc::reconstruct
(
(
- ghf*fvc::snGrad(rho)
- fvc::snGrad(p_rgh)
)*mesh.magSf()
)
);
fvOptions.correct(U);
K = 0.5*magSqr(U);
}
fvOptions.correct(U);
The source code of the acceleration resulting from the description in a moving frame of reference can be found in the following src/finiteVolume/cfdTools/general/MRF/MRFZoneList.C
Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt ( const volScalarField& rho, const volVectorField& U ) const { return rho*DDt(U); } Foam::tmp<Foam::volVectorField> Foam::MRFZoneList::DDt ( const volVectorField& U ) const { tmp<volVectorField> tacceleration ( new volVectorField ( IOobject ( "MRFZoneList:acceleration", U.mesh().time().timeName(), U.mesh() ), U.mesh(), dimensionedVector(U.dimensions()/dimTime, Zero) ) ); volVectorField& acceleration = tacceleration.ref(); forAll(*this, i) { operator[](i).addCoriolis(U, acceleration); } return tacceleration; }
The calculation of the Coriolis force is done in the file src/finiteVolume/cfdTools/general/MRF/MRFZone.C
void Foam::MRFZone::addCoriolis ( const volVectorField& U, volVectorField& ddtU ) const { if (cellZoneID_ == -1) { return; } const labelList& cells = mesh_.cellZones()[cellZoneID_]; vectorField& ddtUc = ddtU.primitiveFieldRef(); const vectorField& Uc = U; const vector Omega = this->Omega(); forAll(cells, i) { label celli = cells[i]; ddtUc[celli] += (Omega ^ Uc[celli]); } }
Note the the function fvc::reconstruct reconstructs a vector defined at the cell centre P 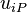 from its face fluxes
from its face fluxes 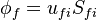 using following expression:
using following expression:
![u_{iP} =\left( \sum_f \frac{S_{fi}S_{fi}}{|S_{fi} |} \right)^{-1}\left [ \sum_f \phi_f \frac{S_{fi} }{|S_{fi} |} \right]](/images/math/b/1/a/b1ad0b0320aec770a0e1b3ea89914616.png) | (x) |
According to [2] it can be shown that the above equation is the solution to following minimization problem:
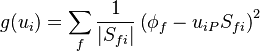 | (x) |
The reconstruction formula used is first order accurate [3]. It's obvious that the effect of the summation over the faces is to smooth out the gradients and therefore to suppress oscillation.
2.1.3 Energy conservation
The energy equation can be found in: https://cfd.direct/openfoam/energy-equation/
The total energy of a fluid element can be seen as the sum of kinetic energy 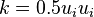 and internal energy
and internal energy  .
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
.
The rate of change of the kinetic energy within a fluid element is the work done on this fluid element by the viscous forces, the pressure and eternal volume forces like the gravity:
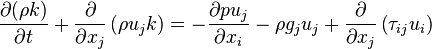 | (3) |
The rate of change of the internal energy  of a fluid element is the heat transferred to this fluid element by diffusion and turbulence
of a fluid element is the heat transferred to this fluid element by diffusion and turbulence 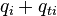 plus the
heat source term
plus the
heat source term  plus the heat source by radiation
plus the heat source by radiation  :
:
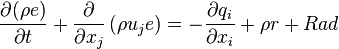 | (4) |
The change rate of the total energy is the sum of the above two equations:
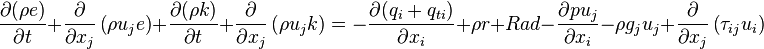 | (5) |
Instead of the internal energy  there is also the option to solve the equation for the enthalpy
there is also the option to solve the equation for the enthalpy 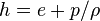 :
:
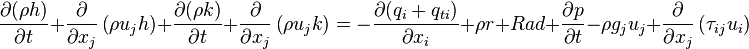 | (5) |
The source code can be found in EEqn.H:
{ volScalarField& he = thermo.he(); fvScalarMatrix EEqn ( fvm::ddt(rho, he) + fvm::div(phi, he) + fvc::ddt(rho, K) + fvc::div(phi, K) + ( he.name() == "e" ? fvc::div ( fvc::absolute(phi/fvc::interpolate(rho), U), p, "div(phiv,p)" ) : -dpdt ) - fvm::laplacian(turbulence.alphaEff(), he) == rho*(U&g) + rad.Sh(thermo, he) + Qdot + fvOptions(rho, he) ); EEqn.relax(); fvOptions.constrain(EEqn); EEqn.solve(); fvOptions.correct(he); thermo.correct(); rad.correct(); Info<< "Min/max T:" << min(thermo.T()).value() << ' ' << max(thermo.T()).value() << endl; }
2.1.4 Species conservation
In order to account for the chemical reactions occurring between different chemical species a conservation equation for each species k has to be solved:
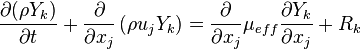 | (6) |
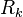 is the reaction rate of the species k.
is the reaction rate of the species k.
The source code can be found in YEqn.H:
tmp<fv::convectionScheme<scalar>> mvConvection(nullptr); if (Y.size()) { mvConvection = tmp<fv::convectionScheme<scalar>> ( fv::convectionScheme<scalar>::New ( mesh, fields, phi, mesh.divScheme("div(phi,Yi_h)") ) ); } { reaction.correct(); Qdot = reaction.Qdot(); volScalarField Yt ( IOobject("Yt", runTime.timeName(), mesh), mesh, dimensionedScalar("Yt", dimless, 0) ); forAll(Y, i) { if (i != inertIndex && composition.active(i)) { volScalarField& Yi = Y[i]; fvScalarMatrix YiEqn ( fvm::ddt(rho, Yi) + mvConvection->fvmDiv(phi, Yi) - fvm::laplacian(turbulence.muEff(), Yi) == reaction.R(Yi) + fvOptions(rho, Yi) ); YiEqn.relax(); fvOptions.constrain(YiEqn); YiEqn.solve(mesh.solver("Yi")); fvOptions.correct(Yi); Yi.max(0.0); Yt += Yi; } } if (Y.size()) { Y[inertIndex] = scalar(1) - Yt; Y[inertIndex].max(0.0); } }
2.1.5 Pressure equation
A good explanation of the derivation of the pressure correction equation for incompressible flows can be found in the book [4]. The purpose is to correct the velocity field and via the equation of state also the density, in order to have a velocity and density field which satisfy the continuity equation. The derivation of this pressure equation can be found in [5]. or also following the link https://feaweb.aub.edu.lb/research/cfd/pdfs/publications/Algorithms-1.pdf.
The equation reads in semi discrete form:
![\frac{ \partial \rho}{\partial t} V_P + \sum_f \psi p v_f ^* \cdot S_f + \sum_f \rho_f^* \frac{\bold{H[v^*]}}{\bold{A_P}} \cdot S_f -
\sum_f \frac{\nabla p_P}{\bold{A_P}} \cdot S_f - \sum_f \rho_f^*v_f^* \cdot S_f + \sum_f \rho_f^* \frac{\bold{H[v']}}{\bold{A_P}} \cdot S_f +
\sum_f \rho_f^'v_f^' \cdot S_f
= 0](/images/math/a/5/d/a5d314f43ae1b66666e58fd151b15a00.png) | (x) |
The density 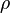 can be written as:
can be written as:
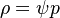 | (x) |
The sum is taken over the faces of the cell with the centre point P.
The last term in the above equation is very small and hence neglected. The second last term is also neglected since the velocity correction 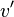 is not know a the moment of the
solution of the equation. Hence the final form of the pressure equation reads:
is not know a the moment of the
solution of the equation. Hence the final form of the pressure equation reads:
![\frac{ \partial \rho}{\partial t} V_P + \sum_f \psi p v_f ^* \cdot S_f + \sum_f \rho_f^* \frac{\bold{H[v^*]}}{\bold{A_P}} \cdot S_f -
\sum_f \frac{\nabla p_P}{\bold{A_P}} \cdot S_f - \sum_f \rho_f^*v_f^* \cdot S_f
= 0](/images/math/4/c/e/4ce3b5c5a9d883a387e90ad7fa0ac74d.png) | (x) |
The pressure p can be written as
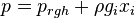 | (x) |
The purpose is the obtain an equation for modified pressure 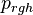 .
Inserting the expression for the pressure in the above equation one obtains:
.
Inserting the expression for the pressure in the above equation one obtains:
![\frac{ \partial \rho }{\partial t} V_P + \sum_f \psi ( p_{rgh} + \rho g_i x_i ) v_f ^* \cdot S_f + \sum_f \rho_f^* \frac{\bold{H[v^*]}}{\bold{A_P}} \cdot S_f -
\sum_f \frac{\nabla p_{rghP}}{\bold{A_P}} \cdot S_f - \sum_f \frac{\nabla \rho_{P} g_i x_i}{\bold{A_P}} \cdot S_f - \sum_f \rho_f^*v_f^* \cdot S_f
= 0](/images/math/8/b/c/8bc539ca6f1cdb10b308801967c7216d.png) | (x) |
The above equation still contains the density 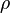 of the current time step. As approximation of the density of the current time step the density of the
previous time step
of the current time step. As approximation of the density of the current time step the density of the
previous time step 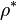 could be used. By doing this and with the following expression:
could be used. By doing this and with the following expression:
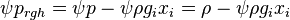 | (x) |
the above equation for the modified pressure could be simplified:
![\frac{ \partial \rho }{\partial t} V_P + \sum_f \psi p_{rgh} v_f ^* \cdot S_f - \sum_f \psi p_{rgh}^* v_f ^* \cdot S_f + \sum_f \rho_f^* \frac{\bold{H[v^*]}}{\bold{A_P}} \cdot S_f -
\sum_f \frac{\nabla p_{rghP}}{\bold{A_P}} \cdot S_f - \sum_f \frac{\nabla \rho^*_{P} g_i x_i}{\bold{A_P}} \cdot S_f
= 0](/images/math/c/3/a/c3a0fcf90dadd675ad0a60e9b4f089ac.png) | (x) |
Comparing the above equation with the source code in the bottom we can identify the corrected phase velocity without considering the pressure gradient as:
![v_f ^* = \frac{\bold{H[v^*]}}{\bold{A_P}} - \frac{\nabla \rho^*_{P} g_i x_i}{\bold{A_P}}](/images/math/e/6/8/e68b99d2135d219f1567b667bc9f4c7b.png) | (x) |
In order to derive the expression for the time derivative in the source code of the pressure equation, the density is divided into the density of the previous time step 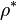 and a density correction
and a density correction 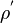 , i.e.,
, i.e., 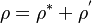 and the time derivative is taken from this expression:
and the time derivative is taken from this expression:
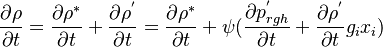 | (x) |
Neglecting the last two terms in the above equation one obtains:
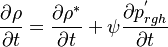 | (x) |
The source code for the pressure equation can be found in pEqn.H:
if (!mesh.steady() && !pimple.simpleRho()) { rho = thermo.rho(); } volScalarField rAU("rAU", 1.0/UEqn.A()); surfaceScalarField rhorAUf("rhorAUf", fvc::interpolate(rho*rAU)); volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p_rgh)); if (pimple.nCorrPISO() <= 1) { tUEqn.clear(); } surfaceScalarField phig(-rhorAUf*ghf*fvc::snGrad(rho)*mesh.magSf()); surfaceScalarField phiHbyA ( "phiHbyA", fvc::flux(rho*HbyA) + MRF.zeroFilter(rhorAUf*fvc::ddtCorr(rho, U, phi)) ); MRF.makeRelative(fvc::interpolate(rho), phiHbyA); const bool closedVolume = adjustPhi(phiHbyA, U, p_rgh); const bool adjustMass = closedVolume && !thermo.incompressible(); phiHbyA += phig; // Update the pressure BCs to ensure flux consistency constrainPressure(p_rgh, rho, U, phiHbyA, rhorAUf, MRF); { fvScalarMatrix p_rghEqnComp ( fvc::ddt(rho) + psi*correction(fvm::ddt(p_rgh)) ); if (pimple.transonic()) { surfaceScalarField phid ( "phid", (fvc::interpolate(psi)/fvc::interpolate(rho))*phiHbyA ); phiHbyA -= fvc::interpolate(psi*p_rgh)*phiHbyA/fvc::interpolate(rho); p_rghEqnComp += fvm::div(phid, p_rgh); } // Thermodynamic density needs to be updated by psi*d(p) after the // pressure solution tmp<volScalarField> psip0(mesh.steady() ? tmp<volScalarField>() : psi*p); while (pimple.correctNonOrthogonal()) { fvScalarMatrix p_rghEqnIncomp ( fvc::div(phiHbyA) - fvm::laplacian(rhorAUf, p_rgh) ); fvScalarMatrix p_rghEqn(p_rghEqnComp + p_rghEqnIncomp); p_rghEqn.setReference ( pressureControl.refCell(), pressureControl.refValue() ); p_rghEqn.solve(mesh.solver(p_rgh.select(pimple.finalInnerIter()))); if (pimple.finalNonOrthogonalIter()) { // Calculate the conservative fluxes phi = phiHbyA + p_rghEqn.flux(); // Explicitly relax pressure for momentum corrector p_rgh.relax(); // Correct the momentum source with the pressure gradient flux // calculated from the relaxed pressure U = HbyA + rAU*fvc::reconstruct((phig + p_rghEqnIncomp.flux())/rhorAUf); U.correctBoundaryConditions(); fvOptions.correct(U); K = 0.5*magSqr(U); } } p = p_rgh + rho*gh; // Thermodynamic density update if (!mesh.steady()) { thermo.correctRho(psi*p - psip0); } } // Update pressure time derivative if needed if (thermo.dpdt()) { dpdt = fvc::ddt(p); } // Solve continuity if (!mesh.steady()) { #include "rhoEqn.H" #include "compressibleContinuityErrs.H" } else { #include "incompressible/continuityErrs.H" } // Pressure limiting const bool pLimited = pressureControl.limit(p); // For closed-volume compressible cases adjust the pressure level // to obey overall mass continuity if (adjustMass) { p += (initialMass - fvc::domainIntegrate(thermo.rho())) /fvc::domainIntegrate(psi); p_rgh = p - rho*gh; } if (adjustMass || pLimited) { p.correctBoundaryConditions(); } // Density updates if (adjustMass || pLimited || mesh.steady() || pimple.simpleRho()) { rho = thermo.rho(); } if (mesh.steady() && !pimple.transonic()) { rho.relax(); } Info<< "Min/max rho:" << min(rho).value() << ' ' << max(rho).value() << endl;
2.2 Equations Solid
For the solid regions only the energy equation has to be solved. The energy equation states that the temporal change of enthalpy of the solid is equal to the divergence of the heat conducted through the solid:
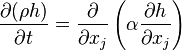 | (7) |
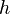 is the specific enthalpy,
is the specific enthalpy, 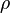 the density and
the density and 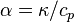 is the thermal
diffusivity which is defined as the ratio between the thermal conductivity
is the thermal
diffusivity which is defined as the ratio between the thermal conductivity 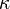 and the specific heat capacity
and the specific heat capacity
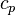 . Note that
. Note that 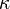 can be also anisotropic.
can be also anisotropic.
The source code can be found in solveSolid.H:
{ while (pimple.correctNonOrthogonal()) { fvScalarMatrix hEqn ( fvm::ddt(betav*rho, h) - ( thermo.isotropic() ? fvm::laplacian(betav*thermo.alpha(), h, "laplacian(alpha,h)") : fvm::laplacian(betav*taniAlpha(), h, "laplacian(alpha,h)") ) == fvOptions(rho, h) ); hEqn.relax(); fvOptions.constrain(hEqn); hEqn.solve(mesh.solver(h.select(pimples.finalIter()))); fvOptions.correct(h); thermo.correct(); Info<< "Min/max T:" << min(thermo.T()).value() << ' ' << max(thermo.T()).value() << endl;
2.3 Coupling between Fluid and Solid
A good explanation of the coupling between fluid and solid can be found in https://www.cfd-online.com/Forums/openfoam-solving/143571-understanding-temperature-coupling-bcs.html.
At the interface between solid s and fluid f the temperature T for both phases that to be the same:
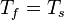 | (8) |
Furthermore the heat flux entering one region at one side of the interphase should be equal to the heat flux leaving the other region on the other side of the domain:
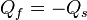 | (9) |
If we neglect radiation the above expression can be written as:
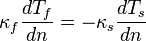 | (10) |
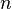 represents the direction normal to the wall.
represents the direction normal to the wall. 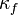 and
and
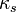 are the thermal conductivity of the fluid and solid, respectively.
are the thermal conductivity of the fluid and solid, respectively.
The source code of the above boundary condition can be found in src/TurbulenceModels/compressible/turbulentFluidThermoModels/derivedFvPatchFields/turbulentTemperatureCoupledBaffleMixed/turbulentTemperatureCoupledBaffleMixedFvPatchScalarField.C
void turbulentTemperatureCoupledBaffleMixedFvPatchScalarField::updateCoeffs() { if (updated()) { return; } // Since we're inside initEvaluate/evaluate there might be processor // comms underway. Change the tag we use. int oldTag = UPstream::msgType(); UPstream::msgType() = oldTag+1; // Get the coupling information from the mappedPatchBase const mappedPatchBase& mpp = refCast<const mappedPatchBase>(patch().patch()); const polyMesh& nbrMesh = mpp.sampleMesh(); const label samplePatchi = mpp.samplePolyPatch().index(); const fvPatch& nbrPatch = refCast<const fvMesh>(nbrMesh).boundary()[samplePatchi]; // Calculate the temperature by harmonic averaging // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ const turbulentTemperatureCoupledBaffleMixedFvPatchScalarField& nbrField = refCast < const turbulentTemperatureCoupledBaffleMixedFvPatchScalarField > ( nbrPatch.lookupPatchField<volScalarField, scalar> ( TnbrName_ ) ); // Swap to obtain full local values of neighbour internal field tmp<scalarField> nbrIntFld(new scalarField(nbrField.size(), 0.0)); tmp<scalarField> nbrKDelta(new scalarField(nbrField.size(), 0.0)); if (contactRes_ == 0.0) { nbrIntFld.ref() = nbrField.patchInternalField(); nbrKDelta.ref() = nbrField.kappa(nbrField)*nbrPatch.deltaCoeffs(); } else { nbrIntFld.ref() = nbrField; nbrKDelta.ref() = contactRes_; } mpp.distribute(nbrIntFld.ref()); mpp.distribute(nbrKDelta.ref()); tmp<scalarField> myKDelta = kappa(*this)*patch().deltaCoeffs(); // Both sides agree on // - temperature : (myKDelta*fld + nbrKDelta*nbrFld)/(myKDelta+nbrKDelta) // - gradient : (temperature-fld)*delta // We've got a degree of freedom in how to implement this in a mixed bc. // (what gradient, what fixedValue and mixing coefficient) // Two reasonable choices: // 1. specify above temperature on one side (preferentially the high side) // and above gradient on the other. So this will switch between pure // fixedvalue and pure fixedgradient // 2. specify gradient and temperature such that the equations are the // same on both sides. This leads to the choice of // - refGradient = zero gradient // - refValue = neighbour value // - mixFraction = nbrKDelta / (nbrKDelta + myKDelta()) this->refValue() = nbrIntFld(); this->refGrad() = 0.0; this->valueFraction() = nbrKDelta()/(nbrKDelta() + myKDelta()); mixedFvPatchScalarField::updateCoeffs(); if (debug) { scalar Q = gSum(kappa(*this)*patch().magSf()*snGrad()); Info<< patch().boundaryMesh().mesh().name() << ':' << patch().name() << ':' << this->internalField().name() << " <- " << nbrMesh.name() << ':' << nbrPatch.name() << ':' << this->internalField().name() << " :" << " heat transfer rate:" << Q << " walltemperature " << " min:" << gMin(*this) << " max:" << gMax(*this) << " avg:" << gAverage(*this) << endl; } // Restore tag UPstream::msgType() = oldTag; }
3 Source Code
4 References
- Jump up ↑ EL ABBASSIA, M.; LAHAYE, D. J. P.; VUIK, C. MODELLING TURBULENT COMBUSTION COUPLED WITH CONJUGATE HEAT TRANSFER IN OPENFOAM.
- Jump up ↑ Aguerre, Horacio J., et al. "An oscillation-free flow solver based on flux reconstruction." Journal of Computational Physics 365 (2018): 135-148.
- Jump up ↑ Aguerre, Horacio J., et al. "An oscillation-free flow solver based on flux reconstruction." Journal of Computational Physics 365 (2018): 135-148.
- Jump up ↑ Moukalled, F., L. Mangani, and M. Darwish. "The finite volume method in computational fluid dynamics." An Advanced Introduction with OpenFOAM and Matlab (2016):
- Jump up ↑ Darwish, F. Moukalled, M. "A unified formulation of the segregated class of algorithms for fluid flow at all speeds." Numerical Heat Transfer: Part B: Fundamentals 37.1 (2000): 103-139


